本文大约 5000 字,阅读大约需要 10 分钟
这是 GAN 学习系列的第二篇文章,这篇文章将开始介绍 GAN 的起源之作,鼻祖,也就是 Ian Goodfellow 在 2014 年发表在 ICLR 的论文—Generative Adversarial Networks”,当然由于数学功底有限,所以会简单介绍用到的数学公式和背后的基本原理,并介绍相应的优缺点。
基本原理
在[GAN学习系列] 初识GAN中,介绍了 GAN 背后的基本思想就是两个网络彼此博弈。生成器 G 的目标是可以学习到输入数据的分布从而生成非常真实的图片,而判别器 D 的目标是可以正确辨别出真实图片和 G 生成的图片之间的差异。正如下图所示:
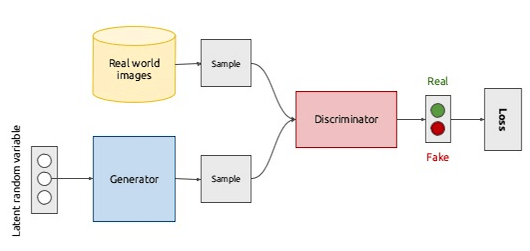
上图给出了生成对抗网络的一个整体结构,生成器 G 和判别器 D 都是有各自的网络结构和不同的输入,其中 G 的输出,即生成的样本也是 D 的输入之一,而 D 则会为 G 提供梯度进行权重的更新。
那么问题来了,如果 D 是一个非常好的分类器,那么我们是否真的可以生成非常逼真的样本来欺骗它呢?
对抗样本
在正式介绍 GAN 的原理之前,先介绍一个概念—对抗样本(adversarial example),它是指经过精心计算得到的用于误导分类器的样本。例如下图就是一个例子,左边是一个熊猫,但是添加了少量随机噪声变成右图后,分类器给出的预测类别却是长臂猿,但视觉上左右两幅图片并没有太大改变。

所以为什么在简单添加了噪声后会误导分类器呢?
这是因为图像分类器本质上是高维空间的一个复杂的决策边界。当然涉及到图像分类的时候,由于是高维空间而不是简单的两维或者三维空间,我们无法画出这个边界出来。但是我们可以肯定的是,训练完成后,分类器是无法泛化到所有数据上,除非我们的训练集包含了分类类别的所有数据,但实际上我们做不到。而做不到泛化到所有数据的分类器,其实就会过拟合训练集的数据,这也就是我们可以利用的一点。
我们可以给图片添加一个非常接近于 0 的随机噪声,这可以通过控制噪声的 L2 范数来实现。L2 范数可以看做是一个向量的长度,这里有个诀窍就是图片的像素越多,即图片尺寸越大,其平均 L2 范数也就越大。因此,当添加的噪声的范数足够低,那么视觉上你不会觉得这张图片有什么不同,正如上述右边的图片一样,看起来依然和左边原始图片一模一样;但是,在向量空间上,添加噪声后的图片和原始图片已经有很大的距离了!
为什么会这样呢?
因为在 L2 范数看来,对于熊猫和长臂猿的决策边界并没有那么远,添加了非常微弱的随机噪声的图片可能就远离了熊猫的决策边界内,到达长臂猿的预测范围内,因此欺骗了分类器。
除了这种简单的添加随机噪声,还可以通过图像变形的方式,使得新图像和原始图像视觉上一样的情况下,让分类器得到有很高置信度的错误分类结果。这种过程也被称为对抗攻击(adversarial attack),这种生成方式的简单性也是给 GAN 提供了解释。
生成器和判别器
现在如果将上述说的分类器设定为二值分类器,即判断真和假,那么根据 Ian Goodfellow 的原始论文的说法,它就是判别器(Discriminator)。
有了判别器,那还需要有生成假样本来欺骗判别器的网络,也就是生成器 (Generator)。这两个网络结合起来就是生成对抗网络(GAN),根据原始论文,它的目标如下:
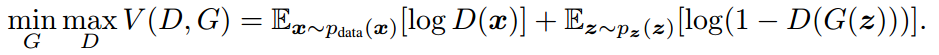
两个网络的工作原理可以如下图所示,D 的目标就是判别真实图片和 G 生成的图片的真假,而 G 是输入一个随机噪声来生成图片,并努力欺骗 D 。
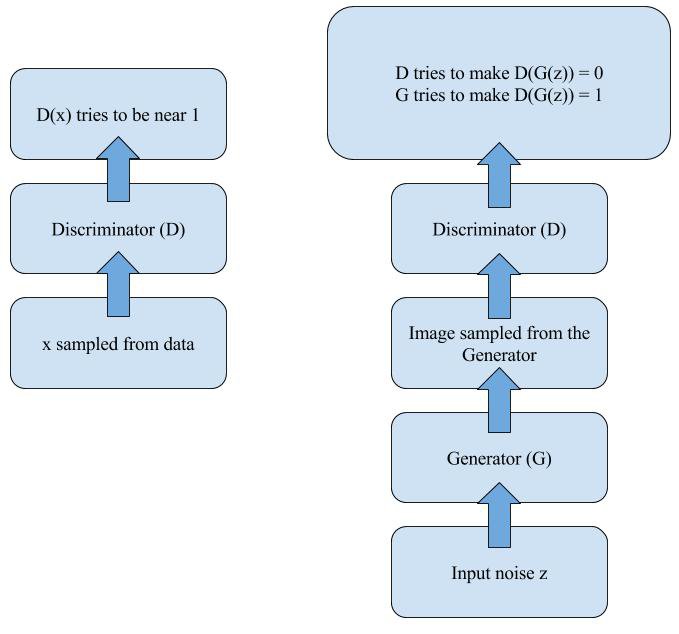
简单来说,GAN 的基本思想就是一个最小最大定理,当两个玩家(D 和 G)彼此竞争时(零和博弈),双方都假设对方采取最优的步骤而自己也以最优的策略应对(最小最大策略),那么结果就已经预先确定了,玩家无法改变它(纳什均衡)。
因此,它们的损失函数,D 的是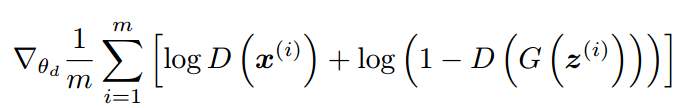
G 的是

这里根据它们的损失函数分析下,G 网络的训练目标就是让 D(G(z)) 趋近于 1,这也是让其 loss 变小的做法;而 D 网络的训练目标是区分真假数据,自然是让 D(x) 趋近于 1,而 D(G(z)) 趋近于 0 。这就是两个网络相互对抗,彼此博弈的过程了。
那么,它们相互对抗的效果是怎样的呢?在论文中 Ian Goodfellow 用下图来描述这个过程:
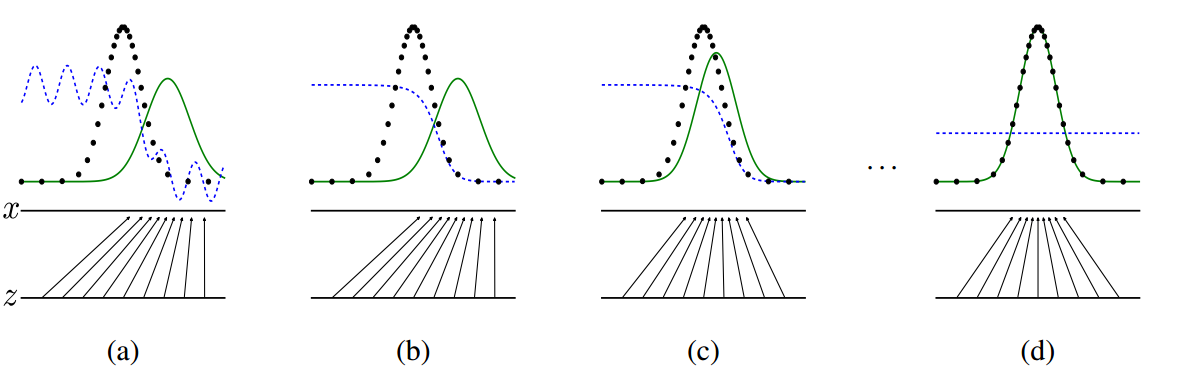
上图中,黑色曲线表示输入数据 x 的实际分布,绿色曲线表示的是 G 网络生成数据的分布,我们的目标自然是希望着两条曲线可以相互重合,也就是两个数据分布一致了。而蓝色的曲线表示的是生成数据对应于 D 的分布。
在 a 图中是刚开始训练的时候,D 的分类能力还不是最好,因此有所波动,而生成数据的分布也自然和真实数据分布不同,毕竟 G 网络输入是随机生成的噪声;到了 b 图的时候,D 网络的分类能力就比较好了,可以看到对于真实数据和生成数据,它是明显可以区分出来,也就是给出的概率是不同的;
而绿色的曲线,即 G 网络的目标是学习真实数据的分布,所以它会往蓝色曲线方向移动,也就是 c 图了,并且因为 G 和 D 是相互对抗的,当 G 网络提升,也会影响 D 网络的分辨能力。论文中,Ian Goodfellow 做出了证明,当假设 G 网络不变,训练 D 网络,最优的情况会是:
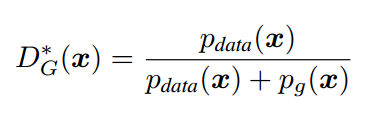
也就是当生成数据的分布 $p_g(x)$ 趋近于真实数据分布 $p_{data}(x) $的时候,D 网络输出的概率 $D_G^*(x)$ 会趋近于 0.5,也就是 d 图的结果,这也是最终希望达到的训练结果,这时候 G 和 D 网络也就达到一个平衡状态。
训练策略和算法实现
论文给出的算法实现过程如下所示:

这里包含了一些训练的技巧和方法:
- 首先 G 和 D 是同步训练,但两者训练次数不一样,通常是 D 网络训练 k 次后,G 训练一次。主要原因是 GAN 刚开始训练时候会很不稳定;
- D 的训练是同时输入真实数据和生成数据来计算 loss,而不是采用交叉熵(cross entropy)分开计算。不采用 cross entropy 的原因是这会让 D(G(z)) 变为 0,导致没有梯度提供给 G 更新,而现在 GAN 的做法是会收敛到 0.5;
- 实际训练的时候,作者是采用 $-log(D(G(z)))$ 来代替 $log(1-D(G(z)))$ ,这是希望在训练初始就可以加大梯度信息,这是因为初始阶段 D 的分类能力会远大于 G 生成足够真实数据的能力,但这种修改也将让整个 GAN 不再是一个完美的零和博弈。
分析
优点
GAN 在巧妙设计了目标函数后,它就拥有以下两个优点。
- 首先,GAN 中的 G 作为生成模型,不需要像传统图模型一样,需要一个严格的生成数据的表达式。这就避免了当数据非常复杂的时候,复杂度过度增长导致的不可计算。
- 其次,它也不需要 inference 模型中的一些庞大计算量的求和计算。它唯一的需要的就是,一个噪音输入,一堆无标准的真实数据,两个可以逼近函数的网络。
缺点
虽然 GAN 避免了传统生成模型方法的缺陷,但是在它刚出来两年后,在 2016 年才开始逐渐有非常多和 GAN 相关的论文发表,其原因自然是初代 GAN 的缺点也是非常难解决:
- 首当其冲的缺点就是 GAN 过于自由导致训练难以收敛以及不稳定;
- 其次,原始 G 的损失函数 $log(1-D(G(z)))$ 没有意义,它是让G 最小化 D 识别出自己生成的假样本的概率,但实际上它会导致梯度消失问题,这是由于开始训练的时候,G 生成的图片非常糟糕,D 可以轻而易举的识别出来,这样 D 的训练没有任何损失,也就没有有效的梯度信息回传给 G 去优化它自己,这就是梯度消失了;
- 最后,虽然作者意识到这个问题,在实际应用中改用 $-log(D(G(z)))$ 来代替,这相当于从最小化 D 揪出自己的概率,变成了最大化 D 抓不到自己的概率。虽然直观上感觉是一致的,但其实并不在理论上等价,也更没有了理论保证在这样的替代目标函数训练下,GAN 还会达到平衡。这个结果会导致模式奔溃问题,其实也就是[GAN学习系列] 初识GAN中提到的两个缺陷。
当然,上述的问题在最近两年各种 GAN 变体中逐渐得到解决方法,比如对于训练太自由的,出现了 cGAN,即提供了一些条件信息给 G 网络,比如类别标签等信息;对于 loss 问题,也出现如 WGAN 等设计新的 loss 来解决这个问题。后续会继续介绍不同的 GAN 的变体,它们在不同方面改进原始 GAN 的问题,并且也应用在多个方面。
参考文章:
- Goodfellow et al., “Generative Adversarial Networks”. ICLR 2014.
- beginners-review-of-gan-architectures
- 干货 | 深入浅出 GAN·原理篇文字版(完整)
- 深度 | 生成对抗网络初学入门:一文读懂GAN的基本原理(附资源)
配图来自网络和论文 Generative Adversarial Networks
以上就是本文的主要内容和总结,可以留言给出你对本文的建议和看法。
欢迎关注我的微信公众号—机器学习与计算机视觉或者扫描下方的二维码,和我分享你的建议和看法,指正文章中可能存在的错误,大家一起交流,学习和进步!

推荐阅读
1.机器学习入门系列(1)—机器学习概览(上)
2.机器学习入门系列(2)—机器学习概览(下)
3.[GAN学习系列] 初识GAN
